FIR 필터를 설계하기 이전에 sampling 을 좀 더 분석해보기로 함.
목차
- 컨볼루션(Convolution) 정의를 쉽게 이해해보자
- 앨리어싱 (Aliasing) 현상에 대해 쉽게 알아보자
- 푸리에 변환(Fourier Transform)에 대해 쉽게 알아보자
- FIR(Finite Impulse Response) Filter에 대해 알아보자
- FIR(Finite Impulse Response) Filter를 설계 해보자 – 1편
- FIR(Finite Impulse Response) Filter를 설계 해보자 – 2편 샘플링(Sampling) – 현재 포스팅
이번 포스팅의 핵심 주제는 Sampling 을 심층 분석 하는 것이다.
수식은 여기 블로그를 참고했으니, 자세한 유도과정은 참고 바란다.
Sampling 에 대해 알아보자.
이전 포스팅은 아날로그처럼 continuous time에 대한 수식이지만, 우리가 디지털 필터를 처리한다면 discrete time으로 처리해야한다. 따라서 이전에 나온 수식을 좀 가공할 필요가 있다.
하지만 그 전에 간단한 전제를 한 가지 가지려고 한다. 이 전제는 푸리에 급수에서 충족하는데, 여기에서 다루지는 않는다.
- 주파수별 삼각함수(sine, cosine)를 조합하면 어떤 주기 신호든 만들 수 있다.
time domain에서 sine wave를 표현해보면 아래와 같다.
x(t) = sin (2 \pi f_0 t) = sin ( w_0 t )
Sampling Time을 T_s 일 때 n번째 sample의 값은 아래와 같다.
x(n) = sin (2 \pi f_0 n T_s ) = sin ( \omega_o n T_s ) = sin( \Omega_o n)
여기서 \Omega_0 = \omega_0 T_s는 [rad]의 unit을 가지고 있다. \omega_0 는 [rad/sec]의 단위를 가지는 것과는 차이를 가지고 있다.
좀 더 깊게 생각해보면 \omega_0 = T_s의 경우만 아니라면 이산 신호를 얻을 수가 있다는 사실을 유추할 수 있다.(앨리어싱 현상을 고려하지 않았을 때 성립할 수 있는 명제이다.)
따라서 어떤 신호 f_0와 샘플링 주파수f_s인 정현파를 f_0 + f_s라고 하자. 이 정현파를 f_s로 샘플링하면 아래와 같은 결과를 얻을 수 있다.
sin (2 \pi (f_0 + f_s) n T_s) = sin ( 2 \pi f_0 n T_s + 2 \pi n f_s T_s )
sin ( 2 \pi f_0 n T_s + 2 \pi n) = sin ( 2 \pi f_0 n T_s )
따라서 어떠한 신호를 해석할 때 샘플링 주파수를 고려하지 않아도 된다.
Discrete form으로 수식을 변경해서 적용해보자.
이제와서 다시 생각해보면, 푸리에 변환 함수를 time domain으로 본 것이 아니고 discrete form으로 다시 변경해서 봐야할 필요가 있다. 이전 포스팅에서 다뤘듯이, 푸리에 변환 함수는 아래와 같다.
F(f) = \int_{-\infty}^{\infty}f(t) e^{-j2{\pi}ft} dt
이걸 Discrete Form으로 변환하면 아래와 같다.(DFT의 함수)
F(k) = \sum_{k=0}^{N-1}f[n] \exp({-j{2{\pi k}\over{N}} n})
변환 과정에 대해서는 푸리에 급수와, 변환에 대한 이해가 선행되어야 한다. 유도 과정을 건너 뛰고 대략적으로 정리하면 아래와 같다.
- 범위를 제한한 것은 실제로 디지털로 처리할 때 샘플을 무한으로 할 수 없기 때문이고, 그래서 샘플의 개수를 N으로 한다.
- 디지털 형태로 바뀌면 2 \pi f -> 2 \pi k / N 로 된다. f의 범위를 0~1로 잡은 것을 대략 유추할 수 있다. 좀 더 깊게 생각하면 N은 한 주기 만큼의 샘플 수를 의미하는 것이라고 유추할 수 있다.
- 한 주기만을 범위로 가져가면 f[n + N] = f[n]으로 신호가 반복되므로, 따라서 함수의 범위를 -\infty - \infty로 잡을 이유가 없어진다.
(푸리에 급수에서는 주기함수라는 전제가 유효하지만, 푸리에 변환으로 가면 굳이 전제를 지킬 필요도 없다. 유도하는 것은 블로그 성격에 맞지 않으므로 생략한다.) - 부록: 1 주기에 대한 주파수 범위를 0~1로 잡을 수도 있지만 negative frequency를 적용한다면 -0.5~0.5로 잡을 수도 있다.
역 변환의 수식은 아래와 같다.
f(n) = {1 \over N} \sum_{k=0}^{N-1} F[k] \exp({j{2{\pi k}\over{N}} n})
Sampling + IDFT를 적용해서 필터를 설계해보자.
그럼 이 수식을 바탕으로 필터를 다시 계산해보자.
샘플은 1024개 이고, Fs = 200, Fc = 40Hz라고 보고, 주기는 -0.5~0.5로 가정해서 rect fucntion을 구해보면 아래와 같다.
f(n) = {1 \over 1024} \sum_{k=-512}^{511} F[k] \exp({j{2{\pi k}\over{1024}} n})
대략 20% 정도만 통과한다고 생각하고 F[k]를 설계하고 plot해보면 아래와 같은 그림이 출력된다.
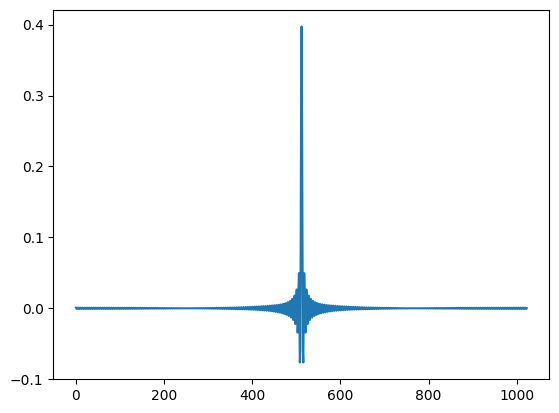
noise가 60Hz고, 원하는 signal은 20Hz라고 했을 때, 입력 신호는 아래와 같다.
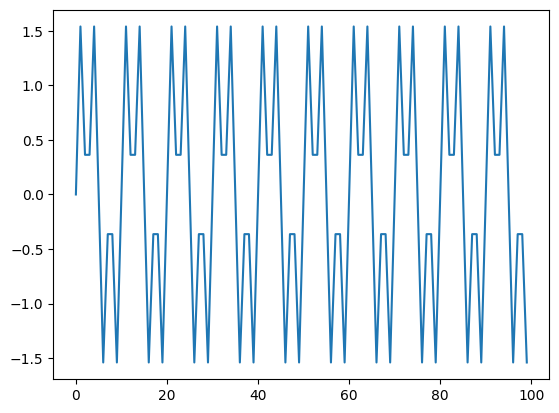
이런 입력 신호가 있다고 할 때, 설계한 filter와 convolution 연산을 하면 기대한 결과가 나와야한다. 기대한 결과가 signal 신호만 출력된 것과 동일하다고 가정하면, 입력과 기댓값, convolution 결과를 같이 plot하면 아래와 같다.
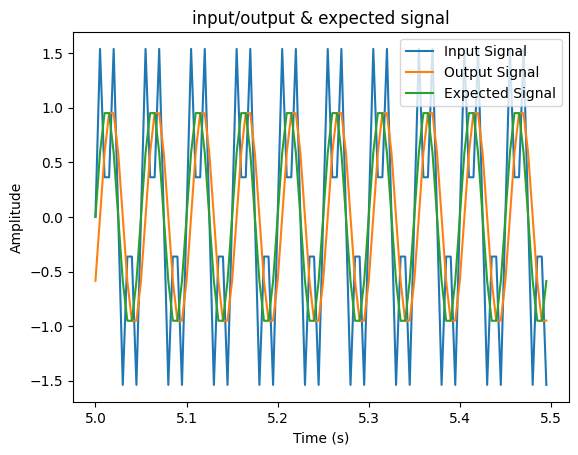
기대한 대로 결과가 잘 나온 것을 볼 수 있다.