목차
- 컨볼루션(Convolution) 정의를 쉽게 이해해보자
- 앨리어싱 (Aliasing) 현상에 대해 쉽게 알아보자
- 푸리에 변환(Fourier Transform)에 대해 쉽게 알아보자
- FIR(Finite Impulse Response) Filter에 대해 알아보자
- FIR(Finite Impulse Response) Filter를 설계 해보자 – 1편 (현재 포스팅)
- FIR(Finite Impulse Response) Filter를 설계 해보자 – 2편 샘플링(Sampling)
FIR 필터 무식하게 설계해보기
FIR 필터를 설계하려면 지난번 포스팅에서 언급한 y(t) = \{ x * h \}(t) = \mathcal{F}^{-1} \{ X \cdot H \} 로 시작해보자.
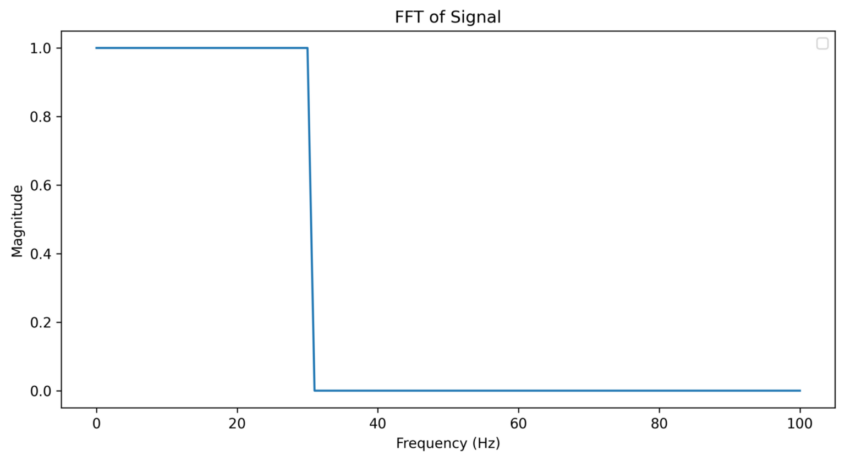
지난번에 언급한것과 같은 window function으로 LPF를 설계하기로 해본다.
그렇다면 위의 window function은 아래와 같을 것이다.(전제는 window가 -20~20hz라고 가정한다. 왜 그런지는 마지막 inverse fft 수식을 보면 알 수 있다.)
H_d(f) = \begin{cases} 1 & \text{if } \lvert{f }\rvert < f_c \\ 0 & \text{else } \end{cases}
이 함수를 역푸리에 변환을 하면 기깔나게 FIR필터로 구현할 수 있을 것이다. 샘플링은 나중 문제고, 일단 time domain으로 변환해서 보자.
아래의 수식은 역 푸리에 변환 수식이다.
h_d(t) = \int_{-\infty}^{\infty} H_d(w) e^{j2 \pi ft}df
= \int_{-f_c}^{f_c} e^{j2 \pi ft}df
= {1 \over {j2\pi t}} [e^{j2 \pi ft}]_{-f_c}^{f_c}
= {1 \over {j2\pi t}} (e^{j2 \pi f_c t } - e^{-j2 \pi f_c t })
여기서 exponential 형태로 되어 있는 두 수식은 오일러 공식을 참고하여 아래와 같이 변경할 수 있다.
= {1 \over {j2\pi t}} (2j sin (2 \pi f_c t) )
= {1 \over {\pi t}} (sin 2 \pi f_c t)
결론으로 나온 함수는 sinc 함수로 표현할 수는 없지만, sinc 함수와 유사한 특성을 가진다고 할 수 있다.
위 결과를 그래프로 그려보자.
cutoff frequency가 10hz라고 했을 때 그래프는 아래와 같이 나온다.
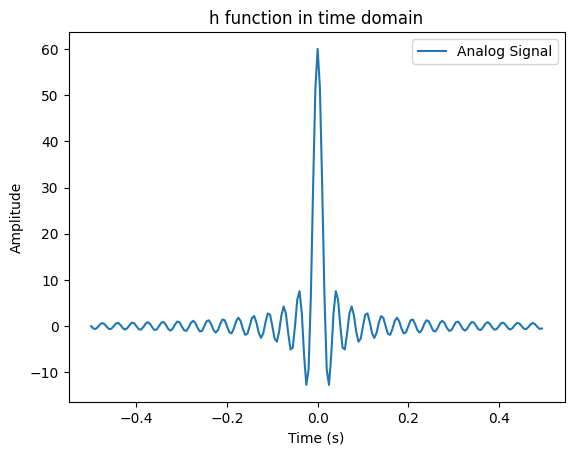
생긴걸 보면 진짜 sinc function과 비슷하다. 저 함수를 FFT로 변환해서 보면 아래와 같다.
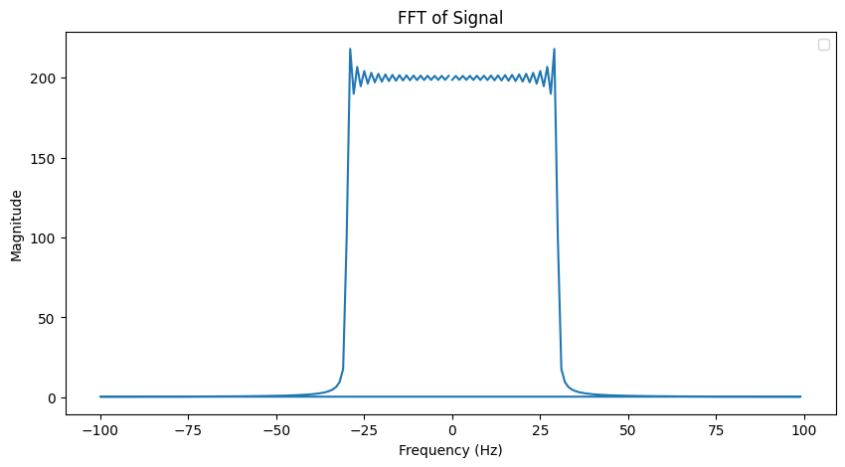
양 옆에 뿔이 솓은 것처럼 보이는 것을 제외하고는 얼추 원하는 필터가 확보 된 것처럼 보인다.
그럼 필터를 적용해보자.
cut off frequency가 30hz로 보고, 노이즈가 50Hz, signal이 20hz로 보자.
입력에는 50Hz와 20Hz 성분이 섞여있고, 필터를 적용한 결과, expected signal인 20hz의 sine wave를 첨부해 비교해 보았다.
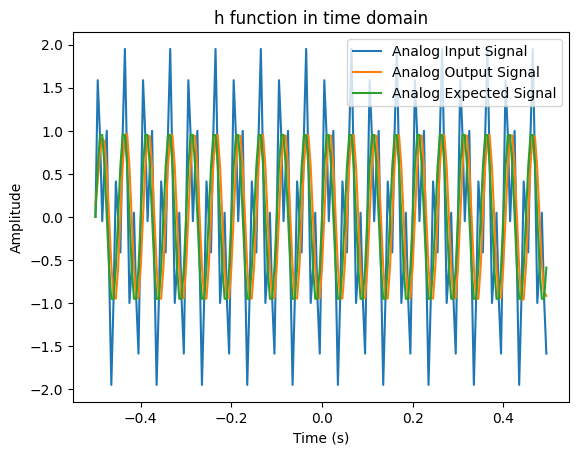
의도한 결과와 비슷하게 나왔다.
이걸로 필터를 잘 만들었으니, FIR 필터도 완성이라고 볼 수 있을까? 아쉽게도 전제가 하나 빠져있다.
설계한 필터는 실제로 적용하지 않는 필터이다.
자세한 것은 다음 포스팅에서 다루겠다.
크 간단명료한 설명과 예제가 매우 훌륭한 글입니다.
나중에 Matched Filter도 해주세요!
요즘은 위키피디아가 참으로 훌륭하더군요 선생님