목차
- 컨볼루션(Convolution) 정의를 쉽게 이해해보자
- 앨리어싱 (Aliasing) 현상에 대해 쉽게 알아보자
- 푸리에 변환(Fourier Transform)에 대해 쉽게 알아보자
- FIR(Finite Impulse Response) Filter에 대해 알아보자(현재 포스팅)
- FIR(Finite Impulse Response) Filter를 설계 해보자 – 1편
- FIR(Finite Impulse Response) Filter를 설계 해보자 – 2편 샘플링(Sampling)
FIR Intro
FIR 필터를 직역하면 주로 ‘유한 임펄스 응답’ 필터라고도 부른다. 이게 무슨 소린가 싶을텐데, 대충 뭐.. 출력이 입력에 영향을 주지 않는 필터라고 보면 된다. 이것도 무슨 소리인가 싶을텐데… 아래의 그림을 보면 이해할 수 있다. 포스팅은 주로 위키를 참고했다.
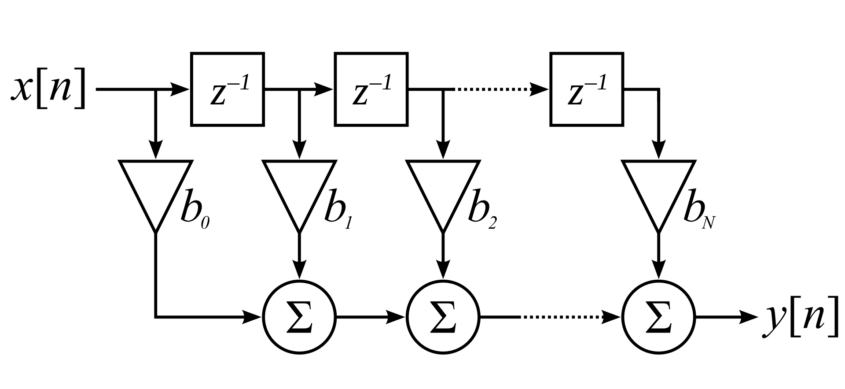
위에서 보는 것처럼 x[n]은 입력이고 모종의 필터를 거친 결과가 y[n]이다. 따라서 y[n]으로부터 x[n]으로 되돌아가는 길이 없으므로 출력이 입력에 영향을 주지 않는 다고 볼 수 있다. 따라서 n차 필터만 지나면 출력이 나오기 때문에 필터는 유한하다. 아니 필터가 그럼 다 유한하지. 무한한 것도 있나? 있지.
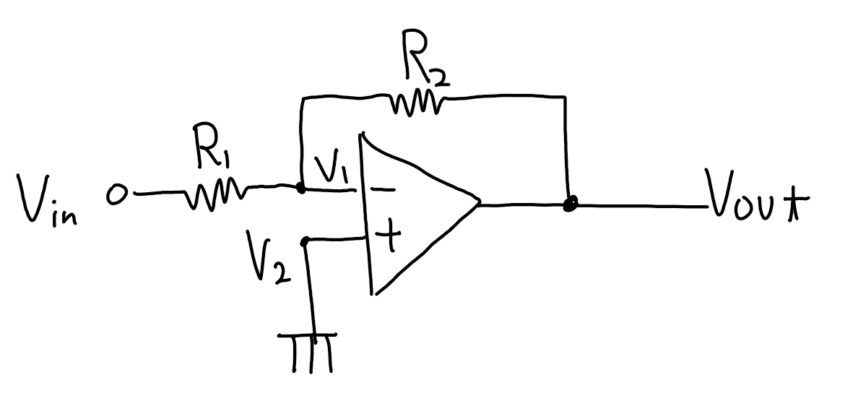
OP AMP로 회로를 꾸미면 위와 같은 그림을 자주 보는데 Vout이 Vin에 영향을 주니까 이건 유한하지 않다. 이걸 응용한게 IIR 필터라고 볼 수 있는데, 그건 기약없는 미래에 다루기로 한다. OPAMP에 대해 궁금하면 이전에 작성한 포스팅을 참고하길 바란다.
그럼 이제 FIR 필터에 대해 배워보자.
FIR Filter 구조 뜯어보기
위에서 봤던 그림을 다시 아래로 붙여놓고 보자.

z^{-1}는 지연을 의미한다. 그러니까 y[n]까지 결과를 미치려면 0에서 N까지만큼 딜레이가 된 입력을 다 더해야 출력을 얻을 수 있는 것이다. 따라서 위 표에 있는 것을 수식으로 정리하면 아래와 같다.
y[n] = b_0 x[n] + b_1 x[n-1] + \cdots + b_N x[n-N]
y[n] = \displaystyle \sum_{i=0}^N b_i \cdot x[n-i]
컨볼루션 수식과도 같은데 그건 이전 포스팅을 참고하시고.. 암튼 생긴건 이런식인데 이게 왜 주파수 필터링이 되느냐? 하는 의문이 생길 수가 있다. 그건 푸리에 변환 수식을 통해 알 수 있는데, 이전 포스팅에서 다루지는 않아서 부가 설명이 필요할 것 같다.
푸리에 변환으로 알아보는 필터링
주파수 관점에서 보자면 아래와 같은 신호가 있다고 가정해보자.
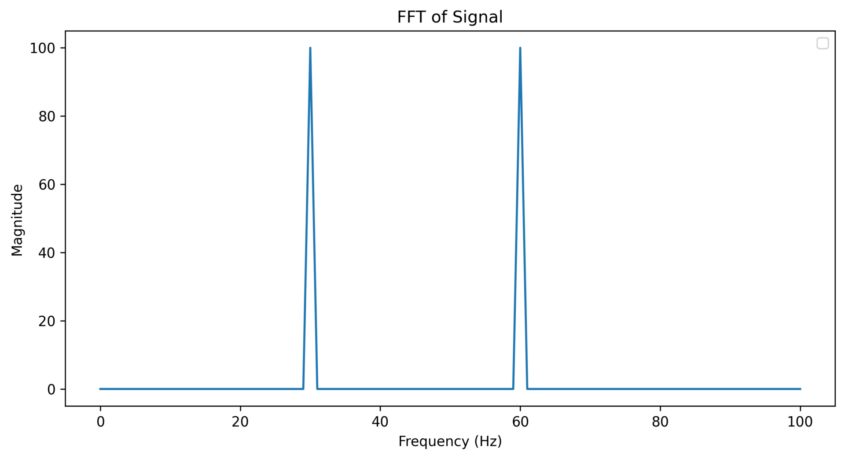
30Hz의 신호와 60Hz의 신호가 있는데 내가 원하는건 30Hz의 신호고 60Hz는 노이즈라고 가정해보자. 이걸 제거하는 방법은 이상적으로 아래와 같은 필터를 만들면 된다.
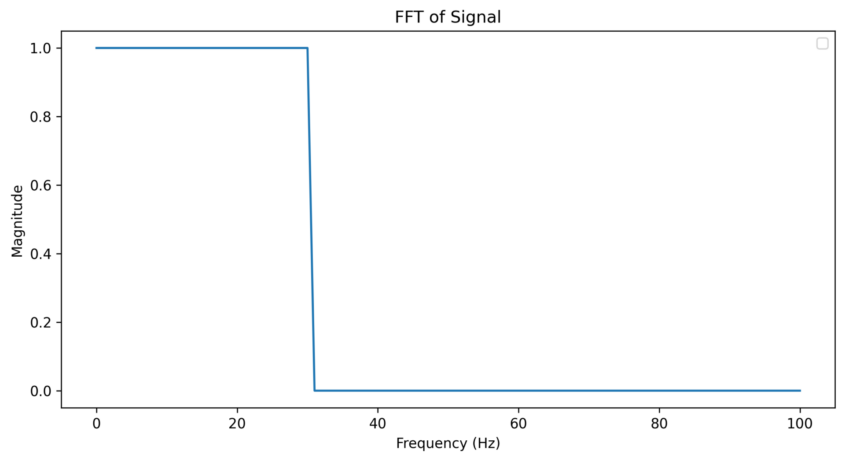
그래서 이걸 대충 둘이 곱해서 plot하면 아래와 같이 필터링이 될 것이다.
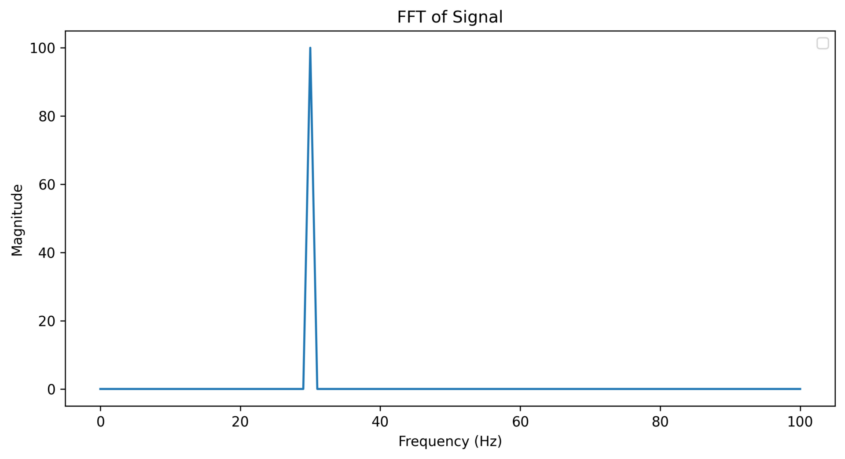
그러니까 정리하면 아래와 같을 것이다.

이걸 수식으로 정리하자면 아래와 같다.
Y[f] = X[f] \times H[f]
아니 뭐.. 위 그림처럼 표현하면 X[f] \times H[f] = Y[f]가 맞을 수도 있겠다. 그게 그거지만. X는 입력 신호의 주파수, H는 필터의 주파수, Y는 출력의 주파수라고 이해하면 된다.
근데 convolution 정리에 따르면 아래와 같은 수식이 있다.
y(t) = \{ x * h \}(t) = \mathcal{F}^{-1} \{ X \cdot H \}
따라서 적절하게 잘 설계한 h를 fft 돌렸을 때 위처럼(H 주파수 대역) 나오기만 한다면 realtime으로 컨볼루션한 결과는 Low Pass Filter의 결과가 나온다는 뜻이다. 이 얼마나 경이로운가.
그럼 FIR 필터에서 h의 계수는 어떻게 구할것인가? 하는 의문이 자연스럽게 생긴다. 이건 다음 포스팅에서 다룰 예정이다.