목차
- 컨볼루션(Convolution) 정의를 쉽게 이해해보자
- 앨리어싱 (Aliasing) 현상에 대해 쉽게 알아보자
- 푸리에 변환(Fourier Transform)에 대해 쉽게 알아보자(현재 포스팅)
- FIR(Finite Impulse Response) Filter에 대해 알아보자
- FIR(Finite Impulse Response) Filter를 설계 해보자 – 1편
- FIR(Finite Impulse Response) Filter를 설계 해보자 – 2편 샘플링(Sampling)
INTRO
이번에는 푸리에 변환에 대해 알아볼 것이다. 푸리에 변환은 주파수 관점에서 신호를 이해하고자 할 때 사용한다. 이를테면 50Hz의 sine wave나 cosine wave를 푸리에 변환하면 50Hz 쪽에 신호의 세기가 나타는 식이다. 우리는 오일러 식으로 주파수를 표현하는 법을 배웠다.
푸리에 변환은 이런 사이트에도 잘 표현되어 있으니, 이 글이 이해가 안가면 해당 글을 참고하라.
오일러 식
오일러 식은 sine, cosine을 exp형식으로 표현 가능하게 만든 식이다. 어떻게 유도되는지를 설명하는건 이번 주제에 어울리지 않으니, 다른 블로그를 참고하길 바란다.
e^{j\theta} = \cos(\theta) + j\sin(\theta)
푸리에 변환은 위와 같은 e^{j\theta}를 조금 변형해서 e^{j2{\pi}ft}형식으로 표현하고, 해당 주파수의 성분을 구할 수 있게 고안된 것이다.
푸리에 변환
푸리에 변환은 아래와 같이 표현된다
F(f) = \int_{-\infty}^{\infty}f(t) e^{-j2{\pi}ft} dt
푸리에 역변환은 아래와 같다.
f(t) = \int_{-\infty}^{\infty}F(f) e^{j2{\pi}ft} df
이것만 보면 이게 무슨 의미가 있나 싶지만, Intro에 서술한 것처럼 적용되는지 확인해보는것 부터 시작하자.
이해해보기
주파수 성분이 f0이고, 크기가 1인 무언가가 있다고 가정해보자. 그럼 아래와 같은 impulse 응답(dirac delta function)처럼 표기 될 수 있다.
F(f) = \delta(2{\pi}f - 2{\pi}f_0)
그럼 이 친구를 역변환한번 해보자.
f(t) = \int_{-\infty}^{\infty}F(f) e^{j2{\pi}ft} df
f(t) = \int_{-\infty}^{\infty} \delta(2{\pi}f - 2{\pi}f_0) e^{j2{\pi}ft} df
그럼 이 친구는 f0에만 성분이 있고, 다른 영역에는 신호가 없으므로 f(x)는 간단하게 도출된다.
f(t) = e^{j2{\pi}f_0t}
여기까지 이해했다면 아주 잘 따라온 것이다.
그럼 FFT로 plot해서 실제로도 이렇게 나오는지 확인해보자.
아래는 50Hz의 exponential 신호를 plot한 것이다.
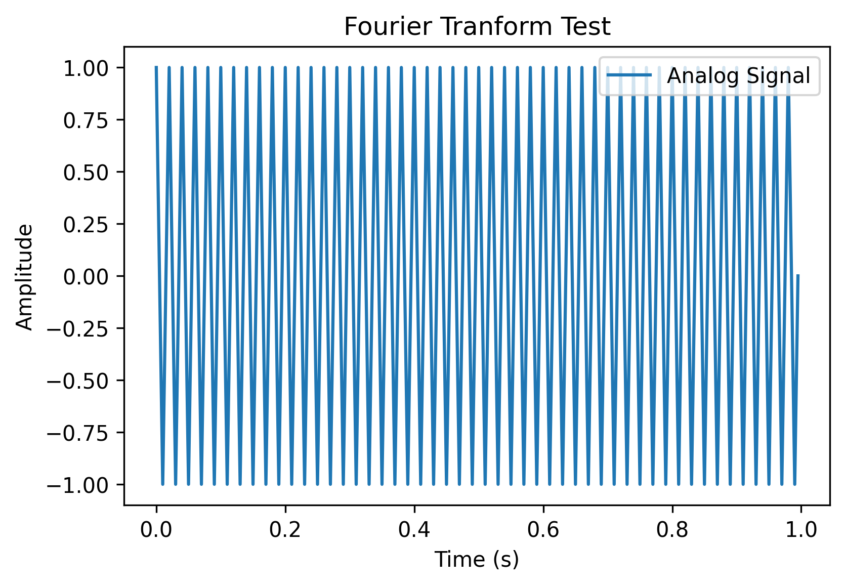
cosine 신호처럼 나온다. 그럼 이 신호를 푸리에 변환해서 plot한 것은 어떻게 나올까?
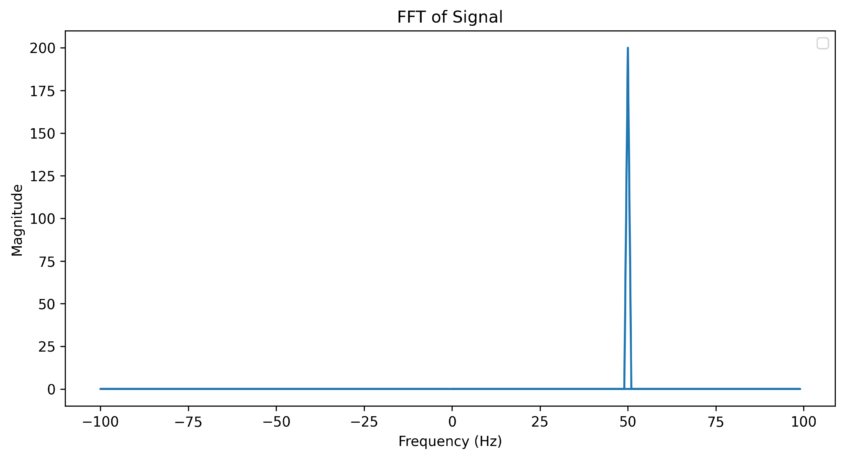
예상한 것처럼 50Hz로 표기된다.
그럼 exponential 신호에 대한 결과를 알았으니, sine wave와 cosine wave에 대한 결과도 알 수 있다.
sine과 cosine wave 푸리에 변환해서 plot해보기
먼저 이해하기 쉽도록 cosine부터 시작해보자. 전에 표기했던 오일러 공식을 변형하면 cosine에 대한 함수를 구할 수 있다.
e^{j\theta} = \cos(\theta) + j\sin(\theta)
e^{-j\theta} = \cos(\theta) + -j\sin(\theta)
여기서 위 두 식을 더하면 아래와 같다.
2\cos(\theta) = e^{j\theta} + e^{-j\theta}
\cos(\theta) = {1 \over 2} (e^{j\theta} + e^{-j\theta})
그럼 이 식을 가지고 푸리에 변환을 헤보자.
\cos(2{\pi}f_{0}t) = {1 \over 2} (e^{j2{\pi}f_{0}t} + e^{-j2{\pi}f_{0}t})
F(f) = \int_{-\infty}^{\infty}f(x) e^{-j2{\pi}ft} dt
F(f) = \int_{-\infty}^{\infty}{1 \over 2} (e^{j2{\pi}f_{0}t} + e^{-j2{\pi}f_{0}t}) e^{-j2{\pi}ft} dt
expoential끼리 곱하면 지수부를 더한 것과 같다.
F(f) = \int_{-\infty}^{\infty}{1 \over 2} {(e^{-j2{\pi}(f - f_{0})t} + e^{-j2{\pi}(f + f_{0}t)})} dt \Leftrightarrow {1 \over 2} (\delta(2{\pi}(f - f_{0})) + \delta(2{\pi}(f + f_{0})))
따라서 -f0에 1/2만큼의 성분이 있고, f0에 1/2만큼의 성분이 있는 것을 확인 할 수 있을 것이다.
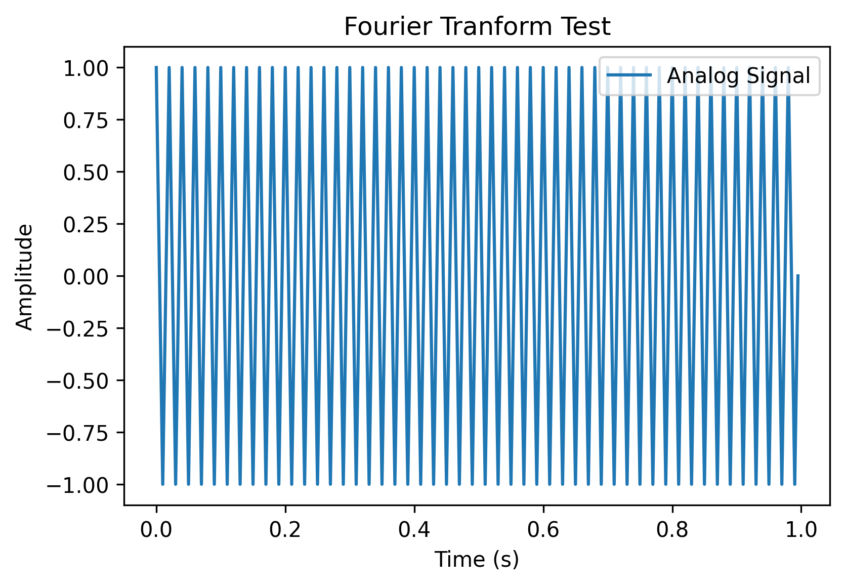
위처럼 cosine 파형을 가지고 변환을 해보자.
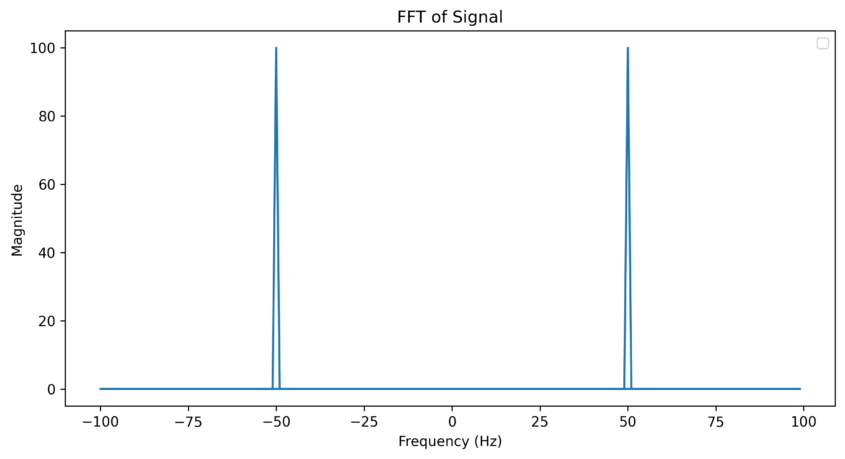
식에서 설명하는 것과 같이 -50에도 성분이 있고, 50에도 성분이 있는 것을 확인할 수 있다. 보통은 -50에 해당되는 negative frequency성분까지 활용하지 않고, fs 200hz 기준 0~100hz positive 성분만 보고 판단한다.
sine wave도 해보자.
e^{j\theta} = \cos(\theta) + j\sin(\theta)
e^{-j\theta} = \cos(\theta) + -j\sin(\theta)
여기서 뺄셈을 하면 아래와 같다.
e^{j\theta} - e^{-j\theta} = 2j\sin(\theta)
\sin(\theta) = {1\over2j}(e^{j\theta} - e^{-j\theta})
같은 과정을 구해보면 아래와 같은 값을 얻는다.
F(f) = \int_{-\infty}^{\infty}{1 \over 2j} {(e^{-j2{\pi}(f - f_{0})t} - e^{-j2{\pi}(f + f_{0}t)})} dt
\Leftrightarrow {1 \over 2j} (\delta(2{\pi}(f - f_{0})) - \delta(2{\pi}(f + f_{0})))
값이 허수로 나와서 멘붕이 올 수 있지만 걱정하지 않아도 된다. 실제로 FFT를 돌려보면 그 결과는 magnitude로 표현되기 때문이다. magnitude는 \sqrt{(real^2 + imagine^2)}임을 참고하라. 아무튼 그래서 결과는 cosine과 같게 나올 것이다.
실제로 한번 돌려보자.
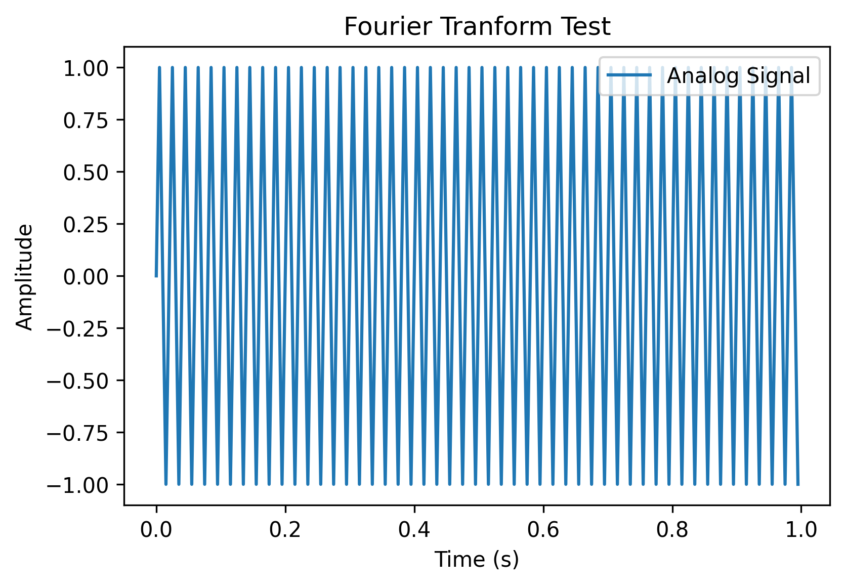
위와 보는 것처럼 sine wave가 생성되었다.
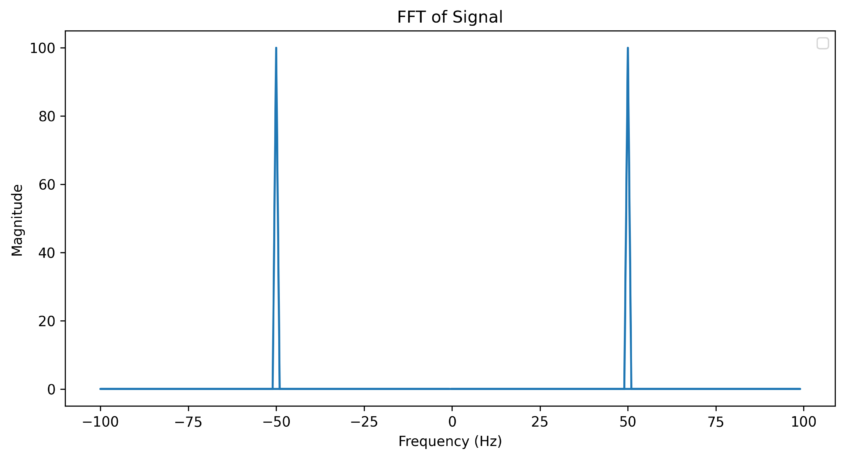
위에서 표기되는 것처럼 sine wave의 magnitude는 cosine과 같은 것을 알 수 있다.
허수 성분이 가지는 의미로도 더 설명할 것이 많지만, 오늘은 크기에 대해서만 포스팅 하겠다.
그럼 오늘 포스팅은 끗.