앨리어싱 (Aliasing) 현상에 대해 쉽게 알아보자

오늘은 오랜만에 신호 처리 관련 포스팅이다.

목차

1. 컨볼루션(Convolution) 정의를 쉽게 이해해보자
2. 앨리어싱 (Aliasing) 현상에 대해 쉽게 알아보자(현재 포스팅)
3. 푸리에 변환(Fourier Transform)에 대해 쉽게 알아보자
4. FIR(Finite Impulse Response) Filter에 대해 알아보자
5. FIR(Finite Impulse Response) Filter를 설계 해보자 – 1편
6. FIR(Finite Impulse Response) Filter를 설계 해보자 – 2편 샘플링(Sampling)

이번에는 시간 관점에서 한번 찍먹해보고, 주파수 관점에선 한번 찍먹해보겠다.
앨리어싱 현상이란 대충 설명하면 샘플링이 그지같이 되어서 각기 다른 신호를 구별해내지 못하는 현상을 의미한다. a를 b로 오인할 수 있다는건데 이게 무슨 소린가? 그냥 아래에 있는 그림을 보면 알 수 있다.

앨리어싱 현상 찍먹해보기

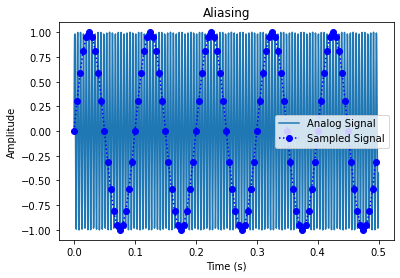
위에서 보는 것처럼 실제 주파수는 디게 높은데, 샘플링을 느리게해서 낮은 주파수의 신호로 오해할 수 있다는거다.
그럼 원 신호를 정확하게 샘플링하려면 적어도 어느정도 되어야하는가?하는 의문이 있을 것이다. 이때 등장하는게 나이퀴스트 주파수라는 희안한 말이 등장한다.

나이퀴스트 주파수

Harry Nyquist

근-엄한 이 분의 이름을 따서 만들어진 것이 나이퀴스트 주파수인데, 이것도 대충 설명하자면 적어도 원 주파수의 2배이상 샘플링 해야한다는 이야기다. 그럼 진짜로 2배이기만 하면 읽을 수 있을까? 싶어서 실험하나 해봤다.

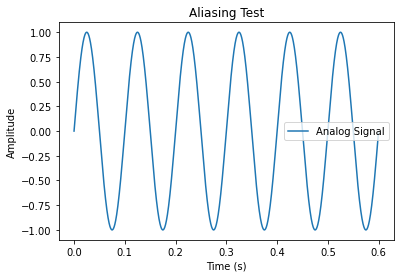
여기 10Hz로 진동하는 sine wave가 있다. 저 아저씨가 구라핑을 찍는지 아닌지 알기 위해 5Hz와 10hz 한번 샘플링 해보겟다.

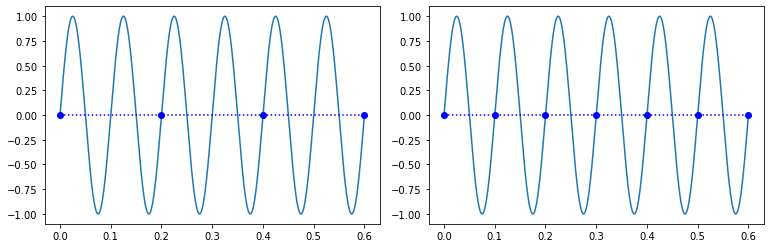
확실히 직선으로 찍히는거 보니까 얼추 이야기가 맞는것 같다. 그럼 2배인 20hz로 찍으면 맞냐?

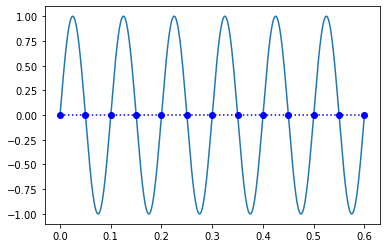
꼭 그렇지만도 않다. 그림에서 보는 것처럼 sine wave에서는 일직선으로 나오기 때문이다.

사실은 나이퀴스트 이론에서 이야기 하는 것은 구체적인 수식이나 증명식이 있는 것은 아니다. 다만 phase가 0인 sine wave가 아니라면 복원이 어느정도 가능한 것으로 보이긴 한다.

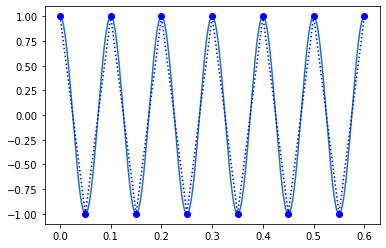
위에 있는 표는 cosine wave로 표기한 것인데, 위와 같은 경우는 얼추 잘 맞는다고도 볼 수 있기 때문이다. 그래서 적어도 2배 이상은 되어야 한다고 표현을 하는듯 하다.
실험치로 정해진 것은 2.56배 이상은 되어야 한다고하더라.

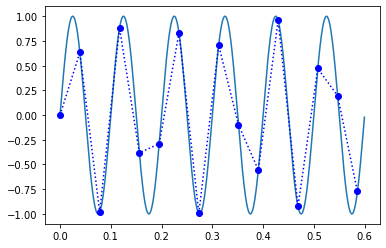
sine wave로 2.56배 이상으로 샘플링 한 것이 위와 같다고 하는데, 실제로 이걸 주파수 도메인에서 보면 어떻게 나오는지 보자.

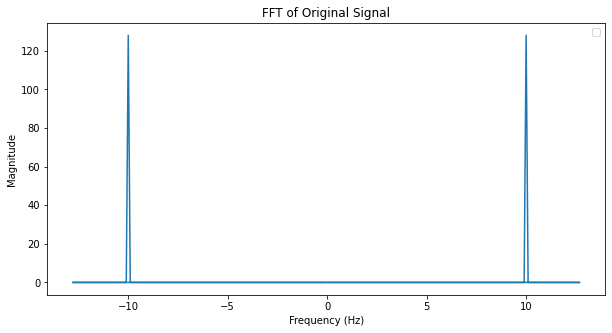
생긴건 이상하게 생겼지만 FFT로 돌려보면 10Hz로 잘 나오는 것을 볼 수 있다.

앨리어싱 뜯어보기

그럼 이제 아래와 같이 210hz의 원신호를 200hz로 샘플링 한 것을 보자.

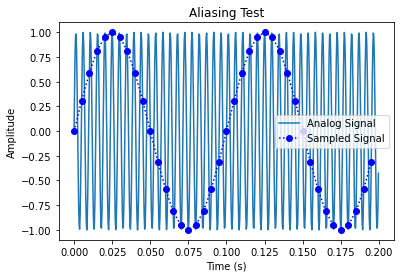
나이퀴스트 이론에 따라 표현할 수 있는 값의 범위는 -100 ~ 100Hz이다.(원 신호를 복원하려면 적어도 2배는 되어야하므로, 표현 가능한 범위도 fs의 1/2이라고 보기 때문이다.) 따라서 주파수 도메인에서는 아래와 같이 표현된다.

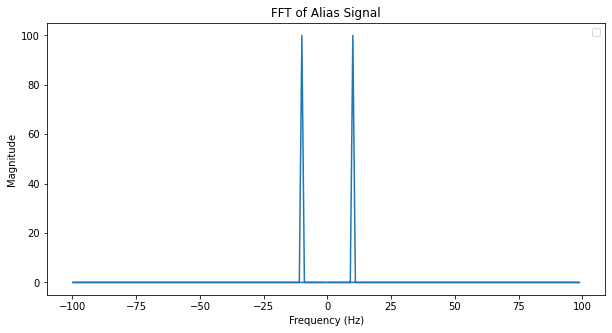
그럼 이게 왜 10Hz이냐? 이건 삼각함수의 주기성을 가지고 증명할 수 있다.
삼각함수는 아래와 같은 주기를 가진다.

\cos(\theta) = \cos(2 \pi k + \theta)

따라서 주파수가 f_{o} + kf_{s}인 정형파를 f_{s}로 샘플링시 아래와 같다.

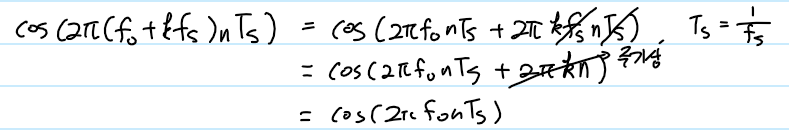
cosine을 시간 형식으로 표현하면 \cos(2\pi ft + \theta)이고 디지털 형식으로 표현하면 \cos(2\pi fnT_{s} + \theta), 여기서 T_{s} = \frac1{f_{s}}인 것임을 유념하라.

이제 여기서 signal이 210이고 fs가 200일 때는 아래와 같이 유도될 것이다.

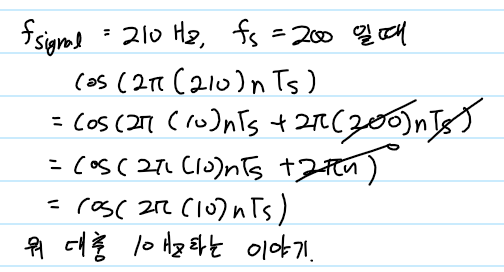
위에 보이는 10이 \cos(2\pi fnT_{s} + \theta) 형식에 적용 했을 때 \cos(2\pi 10nT_{s})이므로, 10hz의 cosine wave임을 알 수 있다.

그럼 반대로 110일 때는 어떻게 되느냐?

90으로 표현이 되는데, 실제로도 그렇게 표현되는지 보자.

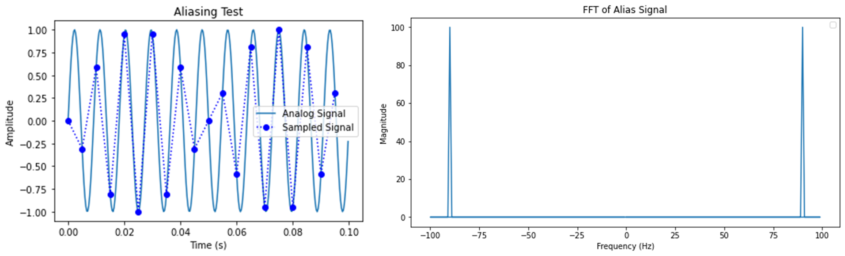
그림은 위에 보이는 것처럼 표현되고 주파수도 90Hz로 표현된다. 이렇게 110Hz(100 + 10)가 pi에 해당되는 100Hz를 기점으로 90Hz(100 – 10)로 표현되는 것을 folding frequency라고 표현하는데, 말그대로 100을 기점으로 접혀서 표현되는 것을 일컫는 말이다. 암튼 그래서 내가 아는 신호의 범위를 알고 있다면 적어도 2배 이상 샘플링을 해야 된다는 결론을 얻을 수 있다.

기회가 되면 다음에는 LPF나 HPF에 대한 포스팅을 해보려 한다. 오늘 포스팅은 여기서 끗.