컨볼루션(Convolution) 정의를 쉽게 이해해보자

목차

1. 컨볼루션(Convolution) 정의를 쉽게 이해해보자(현재 포스팅)
2. 앨리어싱 (Aliasing) 현상에 대해 쉽게 알아보자
3. 푸리에 변환(Fourier Transform)에 대해 쉽게 알아보자
4. FIR(Finite Impulse Response) Filter에 대해 알아보자
5. FIR(Finite Impulse Response) Filter를 설계 해보자 – 1편
6. FIR(Finite Impulse Response) Filter를 설계 해보자 – 2편 샘플링(Sampling)

INTRO

어느날 문득 컨볼루션(Convolution)이 궁금한거다. 위키를 보니 합성곱이라고 정의를 해두긴 했는데, 그러니까 이걸 왜 써먹는지를 설명한다기보단, 수식 전개만 해둔거다.

그러다 구글에 브런치 글을 보았는데, 아우 한국말이 맞나 싶을정도로 이해가 안가더라. 번역 해주신것은 매우 감사하나, 이게 그 뭐랄까. 대학 교재 발번역한 것 돌이켜 보는 기분이랄까.

내 학점을 조진 가장 큰 이유는 대학교재가 개같았기 때문이고, 실전을 경험해보지 못했기 때문이리라.

그래서 원문을 번역해봤다.

난 내가 정말 알고 싶은 것만 번역할거다. 그러니까 더 읽고 싶으면 저 브런치 글을 읽던, 원문을 보던 하시라.

이 글은 콘벌루션 뉴럴 네트워크 이해를 돕기 위해서인거 같은데, 나는 FFT 공부하다가 궁금해진거니까 인공지능은 안다룰꺼고, 그냥 콘벌루션만 다룰거다.

그리고 난 직역 싫어한다. 의역할테니 적당히 걸러서 보기를 부탁드린다. 그리고 난 개인적으로 좀 빡쳐있어서 고삐 풀고 글 좀 쓰려고 한다.

볼 떨구는 걸로 콘벌루션(Convolution) 배워보자

우리가 공을 어느정도 높이에서 떨구는 걸 상상해보자고. 근데 이게 1차원이야. 그러니까 X축만 있다고 생각해보자고. 복잡한거 싫잖아.

X축! X축! 1차원이다. 기억해라

이 가정을 한 상태에서

공을 떨구고, 공이 떨어진 위치에서 다시 공을 집어서 한 번 더 떨굴때 공이 떨어진 거리를 c라고 보자고.

c에 도달할 확률이 얼마나 될까?

하나하나 쪼개서 생각해보자. 공을 떨굴때, 시작 위치에서 떨어진 지점을 a라고 하자. 확률 분포를 f라고 본다면, a지점에 도달할 확률은 f(a)라고 볼 수 있을 것이다.

(주석 : 글에서 다루진 않은것 같지만, 공을 던지는게 아니고 어느정도 높이에서 그냥 놓았을 때를 가정한 것 같다. 던졌다면 그래프가 저렇게 볼록하게 안나올거다.)

처음 떨구고 난 뒤에 a지점에서 공을 다시 주워서 똑같은 짓을 반복한다. 이번 시작 지점에서 떨어진 지점을 b라고 보고 확률 분포를 g라고 보자.

그러면 b지점에 떨어질 확률은 g(b)이 되겠지.

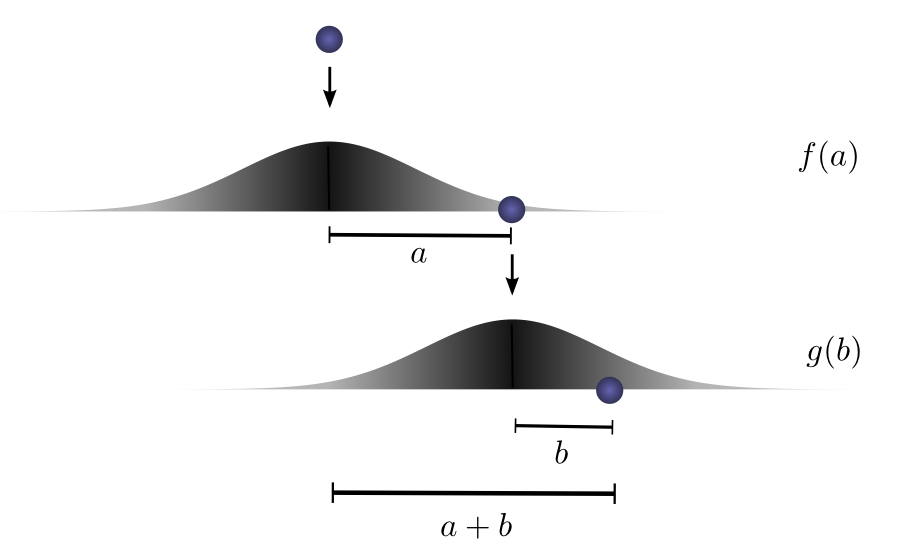
만약에 첫 번째로 떨궜을 때의 결과를 고정값으로 볼 수 있다면, 우리는 거리 a를 알 수 있는거다. 그리고 최종적으로 간 거리 c도 고정 값으로 볼 수 있다면 a + b = c이므로 b의 값도 고정시킬 수 있다. 그렇다면 a지점, b지점에 도달할 확률이 고정되어 있으므로 지점 c에 도달할 확률을 간단히  f(a) \cdot g(b) 로 정리할 수 있다.

그러면 이산 신호로 생각해보자. (시간으로 보면 양이 너무 많으니 간단하게 정수만 생각해보자.) 최종거리 c가 3이라고 정의하자. a = 2 라면 무조건 b = 1이다. a + b = c이기 때문이다.

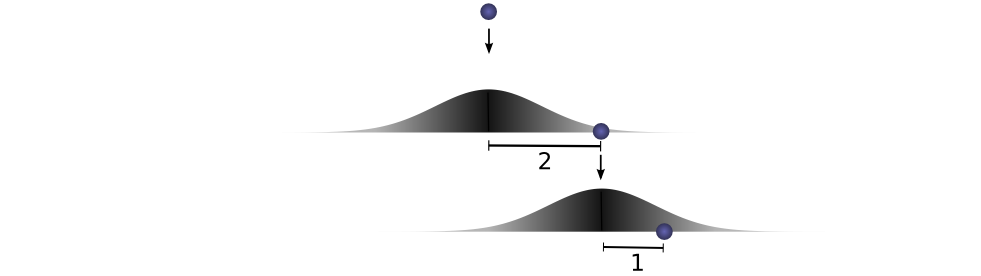
그런데 말입니다

그런데 말입니다

이게 최종 거리 3에 도달하는 유일한 방법은 아니란 말입니다. 처음에는 1만큼 가고 두번째에는 2만큼 갈 수도 있는거고, 아니면 처음엔 0만큼 가고 두번째에 3만큼 갈 수도 있지 말입니다. 뭐가되었건 최종거리가 3이면 된단 말입니다.

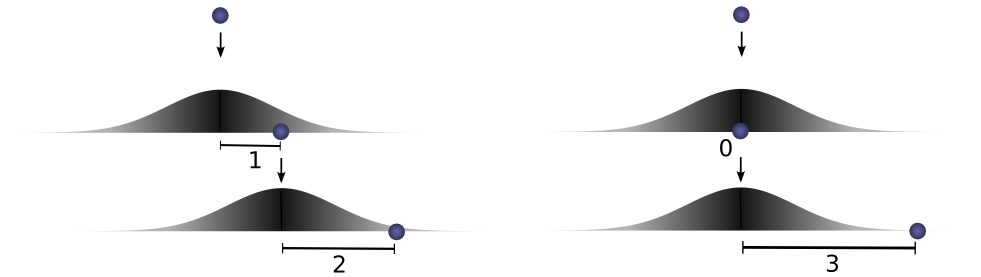
그러니까 각각 f(1) \cdot g(2) , f(0) \cdot g(3) 의 확률도 있는거다.

 결국 3의 지점에 도달 할 수 있는 모든 확률을 다 더해야 최종 지점 3에 도달할 확률을 구할 수 있다.

결국 수식으로 전개하면 아래와 같다.

...\ \ \ \ \ \ \ f(0) \cdot g(3)\ \ \ \ \ \ \ +\ \ \ \ \ \ \ f(1) \cdot g(2)\ \ \ \ \ \ \ +\ \ \ \ \ \ \ f(2) \cdot g(1)\ \ \ \ \ \ \ ...

모든 솔루션을 다 더한다면 한 줄로  요약이 가능하다.

근데 이게 컨볼루션(Convolution)이란 말이다! 특정지어서 이야기를하면 c에 대한 f와 g의 컨볼루션은 아래처럼 정의 된다는거다.

(f*g)(c)= \sum_{a + b = c} {f(a) \cdot g(b)}

근데 위 식에  a도 있고 b도 있으니 컴퓨터로 코딩하면 심히 골룸하단 말이다.

그러니 b = c – a를 적용하면 우리는

(f*g)(c)= \sum_{a} {f(a) \cdot g(c-a)}

를 얻을 수 있다.