Pulse Compression 포스팅
목차
- Matched Filter 알아보기
- Pulse Compression 알아보기(현재 포스팅)
Intro
Pulse Compression은 레이더나, 초음파 등에서 사용하는 필터라고 볼 수 있다. 나는 통신 공학 등을 전공한 것이 아니라서 틀린 정보가 있을 수도 있지만, 재미삼아 이해한 범위까지 정리해보고자 한다.
이전 포스팅에서 Mathced Filter를 다룬 적이 있는데, Pulse Compression에 Matched Filter를 사용하기 때문이다. Matched Filter는 auto-correlation을 적용했지만, 여기서는 cross-correlation을 적용한다. 어차피 기본적인 맥락은 같으니까 별 차이는 없다.
Pulse Compression에서는 보낸 신호가 반사되어서 수신이 되는 경우, 보낸 신호의 정보를 알고 있다면, 반사된 신호와의 cross-correlation을 적용해서 신호의 세기를 알 수 있는 방법이라고 할 수 있다.
관련된 정보는 위키피디아를 참고했다.
Pulse Compression 알아보기
레이더 시스템의 겨우 신호를 보내면 반사가 될텐데, 노이즈가 섞이기 마련이다. matched filter를 사용시 반사된 노이즈가 가우시안 노이즈와 같다면 효율적으로 노이즈를 걸러내고, 신호를 추출할 수 있음을 이전 포스팅에서 정리했다.
pulse compression은 matched filter를 사용해서 range resolution을 높이고 SNR을 높일 수 있는 신호처리 테크닉이다.
일반적으로 특정 시간 동안 sine wave를 보내는 신호가 있다고 가정하자. 이 신호의 반사 신호 r(t)는 s(t)에서 노이즈가 섞인 무언가 일 것이다.
r(t)는 s(t)와 관련 있는 신호일 것이므로 이 둘 신호 간의 cross-correlation을 보면 될 것이다.(이 cross-correlation이 matched filter가 쓰이는 영역일 거고, 하드웨어로 implementation 될 것이다)
그 결과는 위키에서 서술 된 수식에 따라 triangle function으로 귀결된다.
Pulse Compression 결과
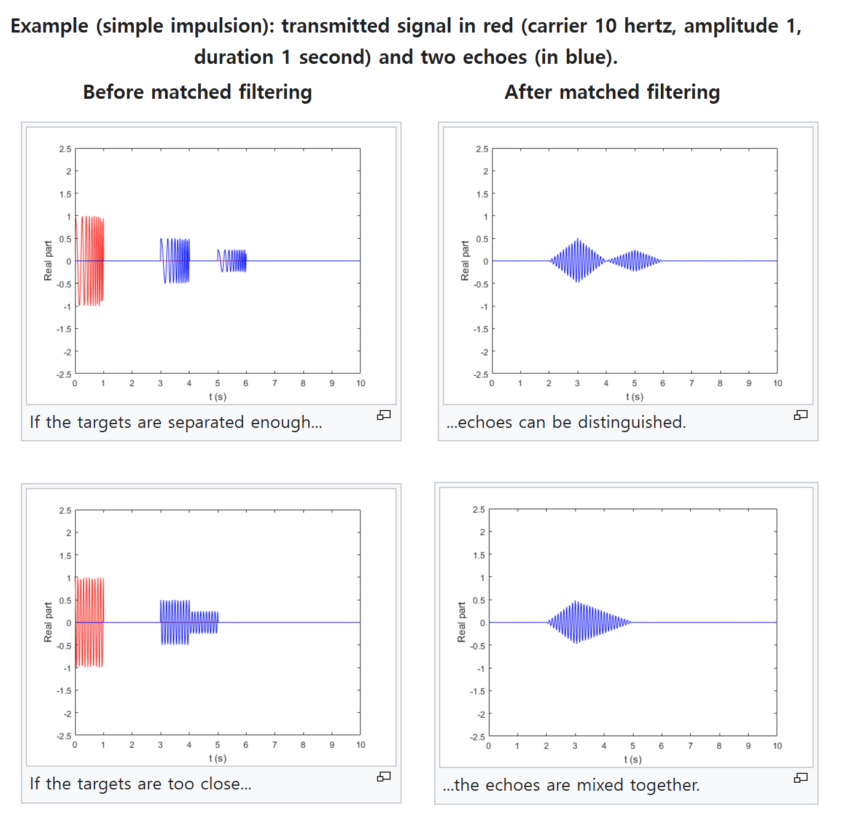
빨간 색 신호가 s(t)이고 파란 신호가 반사된 신호라고 하자(노이즈가 조금 섞였다고 가정하자). 우측은 matched filter 를 거친 결과인데, 송신한 신호와 물체간 거리가 너무 짧다면 우측 하단에서 보는 것과 같이 신호가 섞여 구분할 수 없다. 상기 서술한 range resolution은 이 반사 신호를 구분할 수 있는 최소 거리를 의미한다.
위키에서는 pulse의 길이 – s(t)의 길이가 길수록 SNR은 증가하지만, range resolution은 떨어진다고 이야기 하고 있다. 물체가 멀리있다는 것이 항상 전제가 된다면 신호의 길이가 길어도 되겠지만,(SNR은 증가하고 range resolution은 떨어져도 될 것이므로) target이 짧은 거리에 있다면 문제가 생길 것이다. target의 거리가 짧은데 SNR을 증가시키려면 pulse의 길이를 늘릴 수 없으므로, power를 높여야하겠지만, 현실적으로 어느정도 제약이 있을 수 밖에 없을 것이다.(발열이 증가하기도 하고, 하드웨어 크기도 늘어날 것이고, 단가도 높아질 것이고.. 등등)
난 두 마리의 토끼를 잡고 싶다 이말이야
그렇다면 s(t)를 바꾸면 된다고 되어있다.
linear frequency modulation (or chirping)이라고 시간이 증가하면서 주파수가 증가하는 s(t)를 사용하면 matched filter와 궁합이 아주 좋다.
s(t)와 r(t)의 cross-correlation을 하면 그 출력의 결과가 sinc function으로 되어 있는데, sinc function이라고 하면 중심으로부터 멀어질수록 신호의 크기가 작아지는 특성이 있으므로 일반적인 s(t)를 사용하는 것보다는 sidelobe가 적어 range resolution을 좋게 만들 수 있다.
위에서 보는 것처럼 matched filter를 거친 다음의 결과의 sidelobe가 좁은 것을 볼 수 있다. 나는 이것도 못참겠다? 더 좋은 테크닉이 필요하다? 하면 s(t)에 대해서 hamming window등을 적용하면 약간의 파워 손실은 있겠지만, sidelobe를 더 줄일 수 있다고 되어 있다. 보낼 수 있는 pulse의 길이가 한정되어있는데, SNR은 높고, range resolution을 더 높여야한다면, sidelobe를 줄이는 것이 더 중요하므로, 고려해볼 만 할 것이다.
Stretch processing 부터는 필요한 사람은 wiki를 참고하는게 좋겠다.
APPENDIX
- Noise는 특정 주파수 범위 안에 있다고 전제를 했다. 실제로는 그럴리가 없으니, 보통 1차단에 band pass filter 등을 적용할 것이다.
- r(t)에는 s(t)의 성분과 노이즈인 N(t)의 성분이 섞여 있을 것이다. r(t)에 대한 최종 결과는 Normal Distribution을 가진다고 전제한다. 이 전제가 잘 성립된다면 Matched Filter를 적용 시 아주 기깔나게 r(t)중에 있는 s(t)성분을 잘 detection할 수 있을 것이다.