목차
Matched Filter 알아보는 포스팅이다.
같이 보면 좋은 포스팅 FIR필터 편
블로그는 위키피디아를 참고했다.
생긴건 같은데, 목적에 따라 튜닝이 달라질 수 있는 것이 신호처리의 매력이다.
Intro
디지털 신호처리에서 사용하는 FIR 필터의 모습은 아래와 같다.
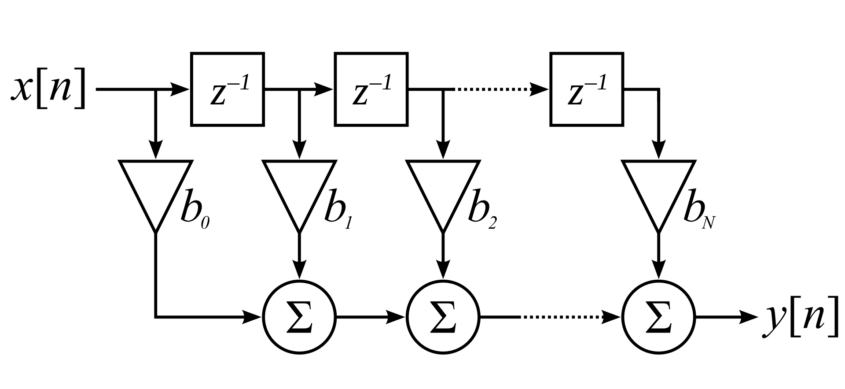
이번에 다룰 Matched 필터의 모습은 모습은 아래와 같다.

놀랍게도 둘이 생긴건 같다. coefficient를 어떻게 튜닝하냐의 차이일 뿐이다. 특이한 점은 FIR필터는 frequncy domain에 따라 처리하는거고, Matched 필터는 time domain의 관점에서 처리하는 필터이다. 푸리에 변환을 통해서 주파수 특성을 분석하고, 주파수 대역에 따라 처리하는 필터와는 달리 노이즈 캔슬링 등에 사용되는 adaptive filter 처럼 통계학적인 요소들을 동원해서 처리하는 필터라고 볼 수 있다. adaptive filter나 다른 PCA 등의 모델에 대해서는 추후에 기회가 되면 포스팅하겠다.
Matched filter 수식 분해
FIR 필터의 모양새와 같다고 주장하는 이유는 수식 때문이다. 수식은 아래와 같다.
y[n] = \displaystyle \sum_{i=-\infty}^\infty h[n-i] \cdot x[n]
물론 -\infty ~ \infty 같은 범위를 정해버리면 실제로는 만들 수 없는 하드웨어가 탄생할 것이다. 현실적으로는 N의 사이즈로 제한하게 될 것이다.
h는 snr을 극대화 할 수 있는 linear filter라고 하자. 그리고 우리가 설계해야하는 건 h이다.
snr을 극대화 한다는 것은 signal & noise 비율을 극대화 한다는 말과 같은 말이다. 따라서 입력신호 x에는 신호와 노이즈가 섞여 있다고 볼 수 있다. x를 정의해보면 아래와 같다.
x = s + v
여기서 s는 신호, v는 첨가된 노이즈라고 하자. 그럼 v의 autocorrelation fucntion을 정의하자. 이해하기 쉽게 노이즈는 가우시안 노이즈라고 하자.
R_v (\tau)=E[ v(t) v_\tau ^H (t - \tau) ]
노이즈 v에 대한 autucorrelation 함수는 가우시안 노이즈이므로 평균 값은 0이고, v^H는 v에 대한 켤레 복소수의 전치 행렬과 같다. 노이즈는 Hermitian matrix임을 참고하도록 하자.
- 가우시안 노이즈는 음수와 양수를 모두 가지고 있을 수 있고 0에 가까울수록 확률이 올라가는 함수라고 보면 된다.
- 헤르미트 행렬은 행렬과 켤레 복소수의 전치 행렬과 값이 같은 행렬을 의미한다. 고유 값이 실수인 장점이 있어 많이 쓰인다.
결과를 y라고 한다면, y에 대한 snr은 아래와 같을 것이다.
SNR = {{\mid y_s \mid^2}\over{E[\mid y_v \mid^2]}}
수식을 더 길게 전개하면 eignvalue를 구한 다음 h를 구할 수 있는데, 자세한건 위키를 참고하면 된다. (수식이 복잡해서 다 이해하진 못했다.)
h = {1 \over {\sqrt{s^H R_v ^{-1} s}}}R_v ^{-1} s
수식에서 추측할 수 있는것은 h는 signal과 random noise에 dependant한 무언가라는 것이다.
더 자세히 section을 읽어보면, h_k = f_{-k} 라는 수식이 하나 튀어 나오는데, 여기서 f는 s의 known sequence(signal model)를 의미한다. 따라서 signal를 flip한 convoltion 형태의 아래 수식을 충족하게 된다.
y[n] = \displaystyle \sum_{k} x[n]h[n-k]
기회가 되면 이를 활용한 pulse compression을 다뤄보겠다.